机器学习概述
常见机器学习模型
无监督学习模型
• 数据聚类(K-means)、数据降维方面的主成份分析( PCA)
有监督学习模型
• 常见的分类模型如:线性分类器、支持向量机、朴素贝叶斯模型、K近邻、决策树等;
• 常见的回归模型如:线性回归、支持向量机回归、K近邻、回归树等
• 定量输出称为回归,或者说是连续变量预测;定性输出称为分类,或者说是离散变量预测。分类模型和回归模型本质一样,分类模型是将回归模型的输出离散化。
几何模型
线性回归
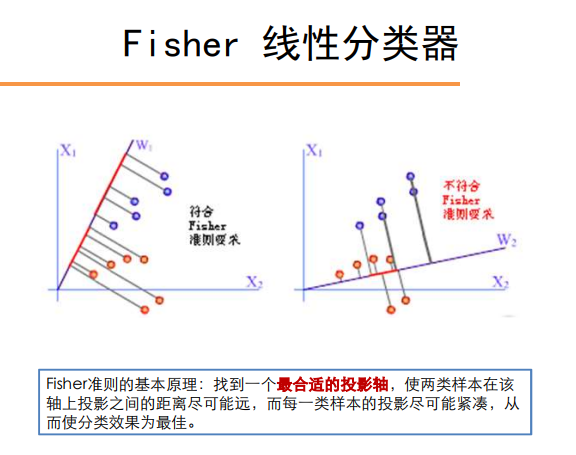
线性分类器
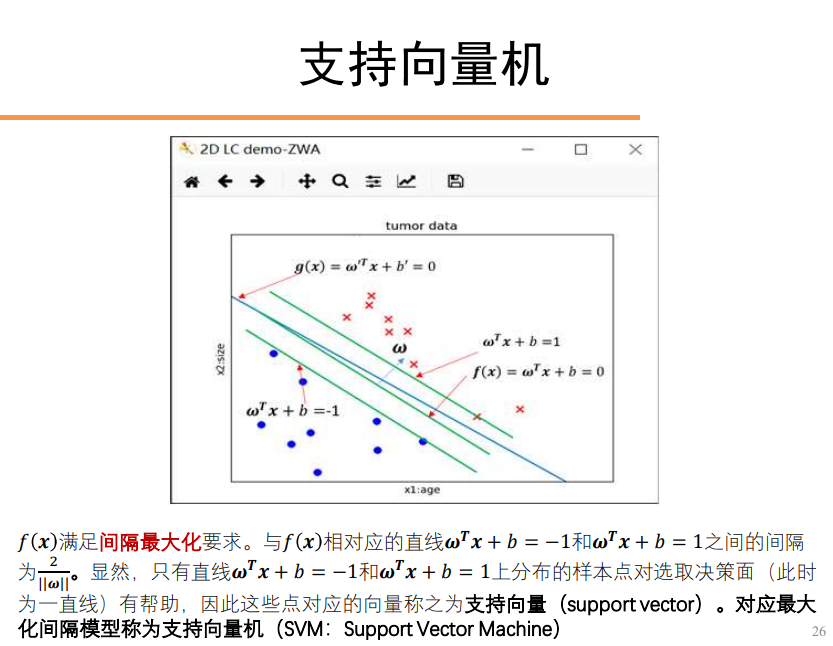
支持向量机
最近邻算法
K近邻算法(KNN)是一种常用的最近邻分类器。
训练阶段,仅仅存储训练数据, 没有显式的学习过程。典型的lazy learning。
判断阶段:(1)选择和输入最近的K个有标签的样本,(2)然后在根据特定规则确定输入的最终分类,如选择概率最大的类作为目标输出,即选择K个样本中“大多数”样本属于的类。
K-均值聚类

改进方法:
- 改变中心点的选择方法:K均值++初始化
- 并行化计算
- Mini-bach K均值
- 减少不必要的距离的计算
神经网络
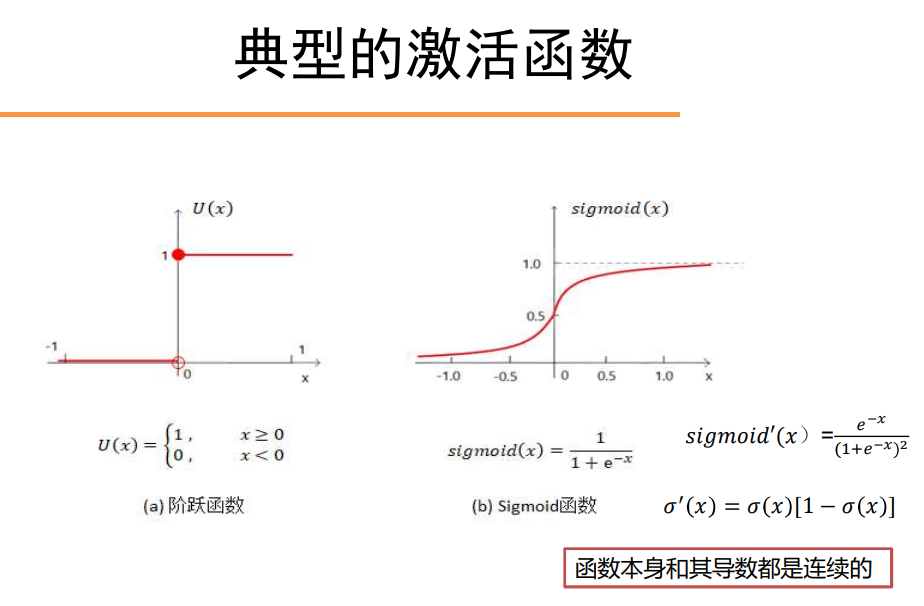
神经元模型
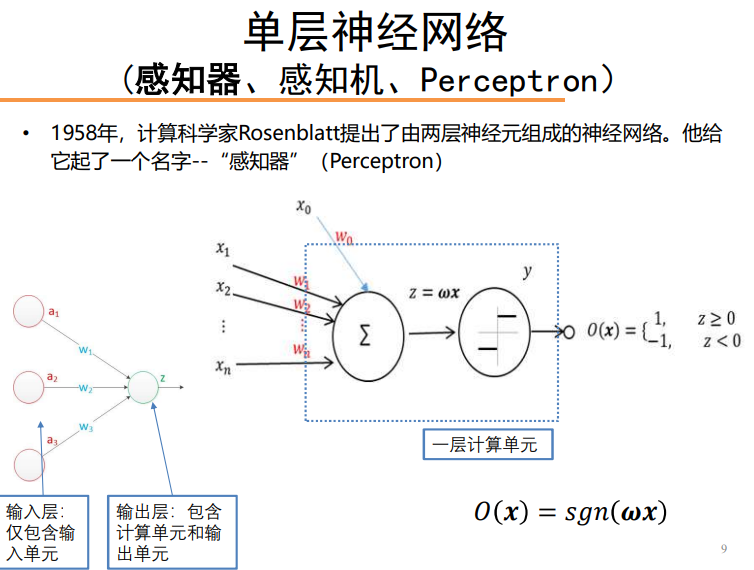
单层神经网络

两层神经网络
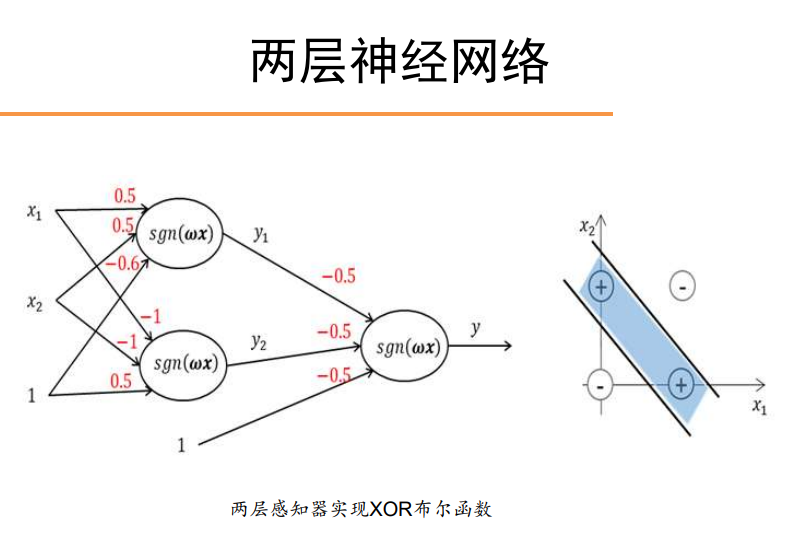
多层网络(BP)
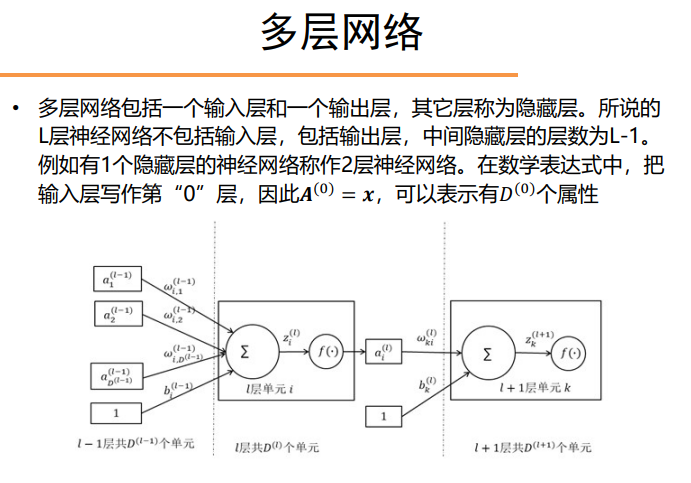

反向传播算法: - 计算第L层偏导
- 计算第L-1层偏导
- 计算其他层偏导
- 调整各层权值矩阵和偏置矩阵
- 迭代训练
反向传播算法详细推导模型评估与选择
测试集和训练集
经验误差与泛化误差
模型在训练集上的误差称为“训练误差”(training error)或者“经验误差”(empirical error)。
在测试集上的误差称为“测试误差”(testing error),在新样本上的误差称为“泛化误差”(generalization error)过拟合和欠拟合
过拟合:泛化误差>测试误差
原因: - 有噪声
- 训练数据量过少
- 模型过于复杂
处理方法: - 早停
- 数据集扩增
- 正则化
- Dropout
- 选择合适的模型
欠拟合:训练误差和测试误差、泛化误差都很大
原因:模型不能很好的捕捉数据特征
处理方法: - 添加其他特征项,特征组合、多项式特征等
- 减少正则化参数
- 增加模型复杂性
测试集数据获取方法
- 留出法
- m折交叉验证
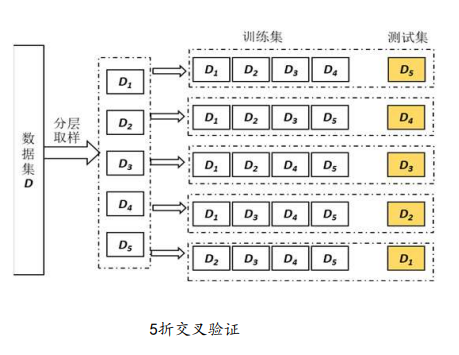
- 自助法:
- 每次随机从D中挑选一个样本,将其拷贝放入D’,然后再将该样本放回原始数据集D中;重复上述步骤,直到我们得到包含M个样本的数据集D’显然,D中有一部分样本会在D’ 中多次出现,而另一部分样本不出现。
模型性能度量



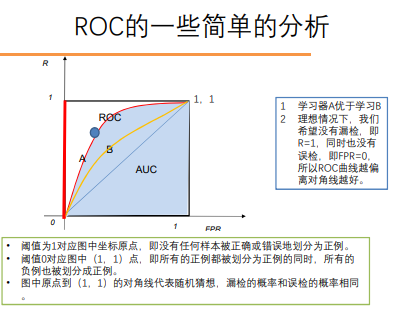
回归模型的泛化误差分解

逻辑模型
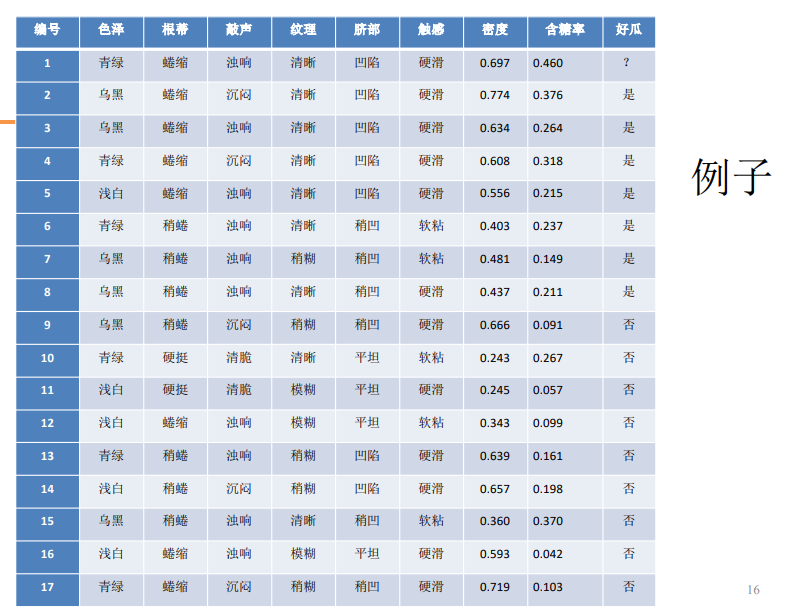
概念学习
概念学习定义为:利用有关某个布尔函数的输入输出训练样例,推断该布尔函数的学习过程。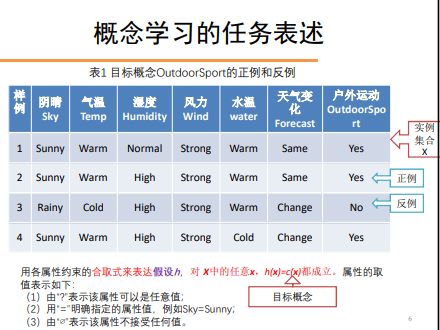

假设空间
假设空间:全部可能的概念构成的空间。
FINDS 算法

决策树

ID3算法



基尼系数

计算学习理论
PAC可学习

VC维
VC维是一种衡量模型学习能力的方法,VC维越高,模型的学习能力通常越强,但也可能越容易过拟合。
想象一下,你有一堆不同颜色的球,你的任务是用一条线(在二维空间中)或一个平面(在三维空间中)将它们分开,红色的在一边,蓝色的在另一边。
- 如果你用一条直线就能完美地分开任何排列的球,那么这个“分开球”的模型的VC维至少是2(因为在二维空间中你需要两个点来定义一条线)。
- 如果你需要一个平面来分开球,那么这个模型的VC维至少是3(因为在三维空间中你需要三个点来定义一个平面)。
假设空间H的VC维就是能够被H打散(数据的随机化处理)的最大示例集的大小。
N维感知器的VC维是N+1概率模型
概率模型的定义和分类
概率模型(probabilistic model)就是将学习任务归结为计算变量的概率分布的机器学习模型。
逻辑斯蒂回归模型是判别概率模型
朴素贝叶斯模型是生成概率模型贝叶斯决策
对于分类任务而言,在知道所有概率分布的理想情况下,贝叶斯决策论是基于概率分布和误判损失选择最优类别标签的基本方法。
计算过程




逻辑斯蒂回归



高斯混合模型

卷积神经网络
卷积运算
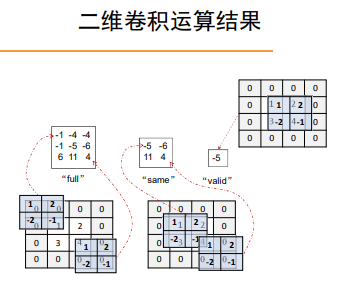
在机器学习中的卷积层的表示
卷积神经网络卷积层常使用的激活函数为ReLU函数。ReLU函数称为整流 函数,定义为
𝑓(𝑥) = max(0, 𝑥)
- Sigmoid激活函数很容易导致梯度消失
- Sigmoid激活函数计算复杂
多层卷积
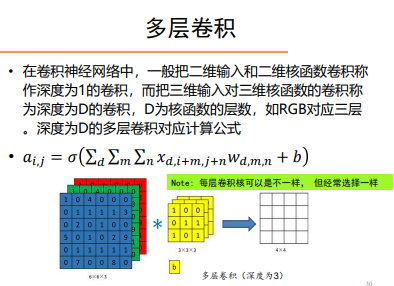
多通道卷积
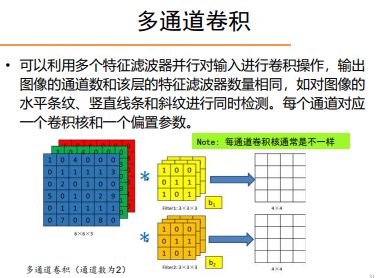
CNN的优势
- 部分连接
- 权值共享
- 多层卷积融合特征
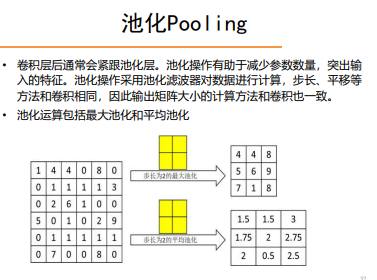
- 可通过池化进一步提取特征,压缩图像
循环神经网络
简单RNN
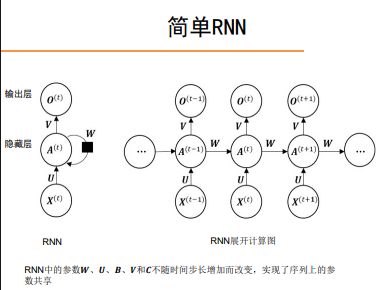
梯度爆炸和梯度消失
梯度消失:梯度在深层网络中反向传播时逐渐变小,直到几乎消失的情况。当梯度变得非常小,它就不再能有效地更新网络的权重,导致学习过程停滞。
解决方法: - 初始化权重,是每个参数的值不要过大或过小
- 使用ReLU代替tanh作为激活函数
- 改变网络结构
梯度爆炸:在网络的反向传播过程中梯度变得异常大。这种情况下,梯度的大值会导致权重更新过猛,使得网络模型无法收敛,甚至可能导致数值计算上的溢出。
解决方法:在算法中设置一个梯度阈值,当梯度超过这个阈值时对梯度进行截取。集成模型
Bagging算法
1)将数据集分成多个不同的子集,子集可以是样本数据集的一部分,也可以是样本特征的一部分;
2)独立使用每个子集分别训练一个弱学习器;
3)集成多个弱学习器的各自决策结果生成最终输出结果。自助采样Bagging算法
- 有放回的随机采样,使得数据具有携带了原始数据分布的能力,又具有多样性。
- 对单个学习器进行训练。
- 采用投票法集成各个学习器的结果(分类问题); 采用均值法集成各个学习器的结果。(回归问题)
随机森林Bagging算法
- 在样本采样的同时还可以引入特征属性采样,进一步增加个体学习器之间的多样性。
- 训练单个学习器。
- 集成。
Boosting算法
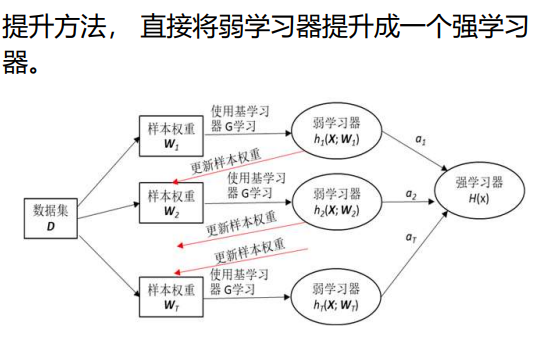
AdaBoost算法
- 初始化训练数据权值分布
- 进行迭代
- 选取误差率最低的弱分类器作为基本分类器,计算误差为e
- 计算权重
- 更新权值分布
- 按弱分类器权重组合各个弱分类器

示例强化学习
Q-Learning算法

SARSA算法


