算法设计与分析期末复习

笔记 期末复习 算法
期末复习
发布日期:   2024-01-09
更新日期:   2024-01-10
文章字数:   3.2k
阅读时长:   14 分
阅读次数:  

第一章

算法复杂性的概念



用特征方程解递归方程的通解


第二章 分治

二分搜索

1
2
3
4
5
6
7
8
9
10
int binarySearch(int a[], int x, int n){
	int left = 0, right = n - 1;
	while(left <= right){
		int middle = (left + right)/2;
		if(x == a[middle]) return middle;
		if(x > a[middle]) left = middle + 1;  //在右半部查找
		else right = middle - 1;              //在左半部查找
	}
	return -1;
}

每执行一次算法的while循环，待搜索数组的大小减少一半。因此最坏情况下，while循环被执行了O(logn)次。循环体内运算需要O(1)时间，因此整个算法在最坏情况下的计算时间复杂性为O(logn)

快速排序

在待排序的数列中，首先找一个数字作为基准数。为了方便，一般选择第 1 个数字作为基准数（。接下来把这个待排序的数列中小于基准数的元素移动到待排序的数列的左边，把大于基准数的元素移动到待排序的数列的右边。这时，左右两个分区的元素就相对有序了；接着把两个分区的元素分别按照上面两种方法继续对每个分区找出基准数，然后移动，直到各个分区只有一个数时为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void quickSort(int a[], int p, int r){
 if(p < r){
	 int q = partition(a, p, r);
	 quickSort(a, p, q-1);
	 quickSort(a, q+1, r);
 }
}
int partition(int a[], int p, int r){
 int i = p,j = r+1;
 int x = a[p];
 while(true){
	 while(a[++i]<x);
	 while(a[--j]>x);
	 if(i > j) break;
	 swap(a[i], a[j]);
 }
 a[p] = a[j];
 a[j] = x;
 return j;
}

最坏时间复杂度：O(n^2)
平均时间复杂度：O(nlogn)
不稳定排序

合并排序

  1. 分解：将原始数组递归地对半分，直到每个子数组只包含一个元素。
  2. 合并：将数组逐步合并，同时进行排序。
    1
    2
    3
    4
    5
    6
    7
    8
    void  MergeSort(int a[], int p, int r){
    	if(p < r){
    		int q = ((p+r)/2);
    		MergeSort(a, p, q);
    		MergeSort(a, q+1, r);
    		Merge(A, p, q, r);
    	}
    }
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    void Merge(int a[], int p, int q, int r){
    	int n1 = q-p+1, n2 = r-q;
    	int L[n1+2], R[n2+2];
    	for(int i = 1;i <= n1;i++) L[i] = a[p+i-1];
    	for(int j = 1;j <= n2;j++) R[j] = a[q+j];
    	L[n1+1] = MAX; R[n2+1] = MAX;
    	int i = 1, j = 1;
    	for(int k = p;k <= r;k++){
    		if(L[i] <= R[j]){
    			A[k] = L[i];
    			i++;
    		}else{
    			A[k] = R[j];
    			j++;
    		}
    	}
    }


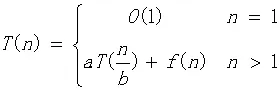
    线性时间选择

    如果能在线性时间内找到一个划分基准，使得按这个基准所划分出的2个子数组的长度都至少为原数组长度的ε倍(0<ε<1是某个正常数)，那么就可以在最坏情况下用O(n)时间完成选择任务，这是线性时间选择问题。
    Pivot/划分基准的选择:
  3. 将n个输入元素划分成 n/5 个组，每组5个元素，只可能有一个组不是5个元素。用任意一种排序算法，将每组中的元素排好序，并取出每组的中位数，共 n/5 个。
  4. 递归调用select来找出这 n/5 个元素的中位数。如果 n/5 是偶数，就找它的2个中位数中较大的一个。
  5. 以这个元素作为划分基准。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    Type select(Type a[], int p, int r, int k){
    	if(r - p < 75){
    		BubbleSort(a,p,r);
    		return a[p+k-1];
    	}
    	for(int i = 0;i <= (r-p-4)/5;i++){
    		BubbleSort(a, p+5*i, p+5*i+4);
    		Swap(a[p+i],a[p+5*i+2]);
    	}
    	Type x = selct(a, p, p+(r-p-4)/5,(r-p-4)/10);
    	int i = Partition(a, p, r, x);
    	int j = i-p+1;
    	if(k <= j) return Select(a, p, i, k);
    	else return Select(a, i+1, r, k-j);
    }

    循环赛

    按照分治策略，将所有选手分为两半，n个选手的比赛日程表就可以通过为n/2个选手设计的比赛日程表来决定，递归地对选手进行分割，直到只剩下2个选手时，比赛日程表的制定就变得很简单，这是只要让这2个选手进行比赛就可以了。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    void Round(A, n){
    	if(n == 1){
    		A[1][1] = 1;
    		return 0;
    	}
    	Round(A,n/2);
    	int m = n/2;
    	for(int i = 1;i <= m;i++){
    		for(int j = 1;j <= m;j++){
    			A[i][j+m] = A[i][j] + m; //填充右上角
    			A[i+m][j] = A[i][j+m]; //将右上角的值复制到左下角
    			A[i+m][j+m] = A[i][j]; //将左上角上的值复制到右下角 
    		}
    	}
    }

    最接近点对

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    //一维
    bool Cpair1(s,d){
    	n = |s|;
    	if(n < 2){
    		d = INFINITE；
    		return false;
    	}
    	m = s中各坐标的中位数；
    	构造S1和S2
    	S1={x<m} S2={x>m}
    	Cpair(s1,d1);
    	Cpair(s2,d2);
    	p = max(s1);
    	q= min(s2);
    	d = min(d1,d2,q-p);
    	return true;
    }

    第三章 动态规划

    最优子结构性质

    原问题的最优解包含了子问题的最优解，即原问题可以由子问题的最优解组合而成，这就使得问题可以拆分成若干个子问题。

    重叠子问题

    每次产生的子问题并不总是新问题，有些子问题被反复计算，这是和分治的不同点。

    动态规划算法设计步骤

  • 找出最优解的性质，并刻画其结构特征
  • 递归地定义最优值
  • 以自底向上的方式计算出最优值
  • 根据计算最优值是得到的信息，构造最优解

    矩阵连乘问题

    计算A[i:j]的最优次序所包含的计算矩阵子链A[i:k]和A[k+1:j]的次序也是最优的。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    void MatrixChain(int *p, int n, int **m, int **s){
    	for(int i = 1;i <= n;i++) m[i][i] = 0;
    	for(int r = 2;r <= n;r++){
    		for(int i = 1;i <= n-r+1;i++){
    			int j = i+r-1;
    			m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];
    			s[i][j] = i;
    			for(int k = i+1;k < j; k++){
    				int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
    				if(t < m[i][j]){
    					m[i][j] =  t;
    					s[i][j] = k;
    				}
    			}	
    		}
    	}
    }
    //输出最优解
    void traceback(int i, int j, int **s){
    	if(i == j)return;
    	traceback(s,i,s[i][j]);
    	traceback(s,s[i][j]+1,j);
    	cout<<"Multiply A"<<i<<","<<s[i][j];
    	cout<<" and A"<<(s[i][j] + 1)<<","<<j<<endl;
    }

    最长公共子序列

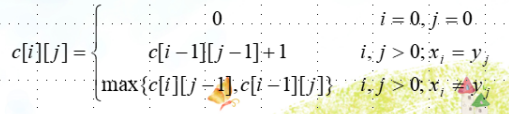
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    void LCSLength(int m, int n, char *x, char *y, int **c, int **b){
    	int i,j;
    	for(i = 1;i <= m;i++) c[i][0] = 0;
    	for(i = 1; i <= n;i++) c[0][i] = 0;
    	for(i = 1;i <= m;i++){
    		for(j = 1;j <= n;j++){
    			if(x[i] == y[j]){
    				c[i][j] = c[i-1][j-1] + 1;
    				b[i][j] = 1;
    			}else if(c[i-1][j] >= c[i][j-1]){
    				c[i][j] = c[i-1][j];
    				b[i][j] = 2;
    			}else{
    				c[i][j] = c[i][j-1];
    				b[i][j] = 3;
    			}
    		}
    	}
    }
    //构造最长公共子序列
    void LCS(int i, int j, char *x, int **b){
    	if(i == 0||j == 0) return;
    	if(b[i][j] == 1){
    		LCS(i-1, j-1, x, b);
    		cout<<x[i];
    	}else if(b[i][j] == 2){
    		LCS(i-1, j, x, b)
    	}else
    		LCS(i,j-1,x,b)
    }

    利用最长公共子序列求解最长递减子序列

    利用最长公共子序列求解回文词的构造

    最大子段和

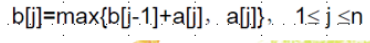
    1
    2
    3
    4
    5
    6
    7
    8
    9
    int maxSum(int n,int *a){
    	int sum = 0,b = 0;
    	for(int i = 1;i <= n;i++){
    		if(b>0) b+=a[i];
    		else b=a[i];
    		if(b>sum) sum = b;
    	}
    	return sum;
    }

    记录起始点与结束点下标

    0/1背包

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    int Knapsack(int n, int c, int w[], int v[], int x[]){
    	int m[n+1][c+1]; //m[i][j]表示考虑前i个物品，背包容量为j时的最大价值
    	for(int j = 0;j <= c;j++) m[0][j] = 0; //没有物品可选
    	for(int i = 1;i <= n;i++){
    		for(int j = 0;j <= c;j++){
    			if(w[i] < j){
    				m[i][j] = max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
    			}else{
    				m[i][j] = m[i-1][j];
    			}
    		}
    	}
    	int j = c;
    	for(int i = n;i > 1;i--){
    		if(m[i][j] == m[i-1][j]){
    			x[i] = 0;
    		}else{
    			x[i] = 1;
    			j -= w[i];
    		}
    	}
    	return m[n][c];
    }
    时间复杂度为O(nc)

    第四章 贪心

    贪心算法的证明

    首先假设存在一个最优解，然后证明存在一个以贪心选择开始的最优解，进一步，在做了贪心选择之后，子问题也是贪心选择获得的最优解。

    活动安排

    先把活动1选上，再依次选择完成时间最早的相容活动
    1
    2
    3
    4
    5
    6
    7
    8
    void GreedySelect(int n, Type s[], Type f[], bool A[]){
    	A[1] = true;
    	int j = 1;
    	for(int i = 2;i <= n;i++){
    		if(s[i] >= f[j]) {A[i] =true; j=i;}
    		else A[i] = false;
    	}
    }

    背包问题

    按照重量和价值比排序，依次装入背包，最后一个不能完全装部分装
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    void Knapsack(int n, float M, float v[], float w[], float x[]){
    	Sort(n,v,w);
    	int i;
    	for(i = 1;i <= n;i++) x[i] = 0;
    	float c = M;
    	for(i=1;i<=n;i++){
    		if(w[i]>c) break;
    		x[i] = 1;
    		c -= w[i];
    	}
    	if((i<=n)&&(c>0)) x[i] = c/w[i];
    }

    哈夫曼编码

    正确性证明

    贪心选择性质

    需要证明：设字符集C={c|f(c)}，x和y是其中具有最小频率f(x)和f(y)的2个字符，则存在C的最优前缀码，使x和y具有相同码长，且只有最后一位编码不相同。
  1. 显然C中只有2个字符时，结论成立

  2. 最优子结构性质

    算法复杂性

    编码字符集中每一字符c的频率为f(c)，共有n个字符。
  3. 以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。
  4. 一旦2棵具有最小频率的树合并后，产生一棵新的树，并将新树插入优先队列Q。
  5. 经过n－1次的合并后，优先队列中只剩下一棵树，即所要求的树T。
  6. 算法用最小堆实现优先队列Q。初始化优先队列需要O(n)计算时间，最小堆的removeMin和put运算均需O(logn)时间，n－1次的合并总共需要O(nlogn)计算时间。
    因此，关于n个字符的哈夫曼算法的计算时间为O(nlogn)

    最小生成树

    Prim算法



    Kruskal算法


    单源最短路径



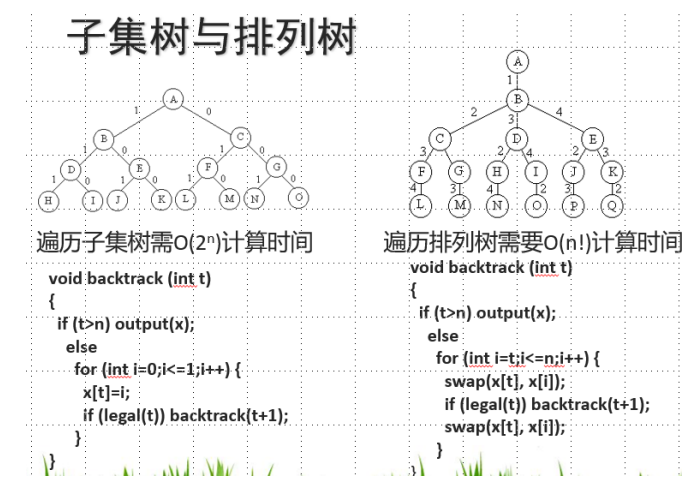
    第五章 回溯法

    时间复杂度

    轮船装载

    尽量装满一艘，然后去装第二艘
    剪枝策略：
    左子树：不超载
    右子树：最优解选择
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    n:集装箱数 bestx:当前最优解
    w:集装箱重量数组 c:第一艘轮船载重量
    cw:当前载重量 bestw:当前最优载重量
    r:剩余集装箱的重量

    void Backtrack(int i){
    	if(i > n){
    		if(cw > bestw){
    			for(int j = 1;j <= n;j++)
    				bestx[j] = x[j];
    			bestw = cw;
    		}
    		return;
    	}
    	r -= w[i];
    	if(cw + w[i] <= c){
    		x[i] = 1;
    		cw += w[i];
    		Backtrack(i+1);
    		cw -= w[i]; 	
    	}
    	if(cw + r > bestw){
    		x[i] = 0;
    		Backtarck(i+1);
    	}
    	r += w[i];
    }
    由于bestx可能被更新O

    旅行售货员

    排列树
    剪枝条件1：如果当前正在考虑的顶点j与当前路径中的末端结点i没有边相连，即w[i,j]=∞,则不必搜索j所在分支
    剪枝条件2：如果B(i)≥bestw,则停止搜索x[i]分支及其下面的层
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    a:邻接矩阵 x:当前路径的顺序
    bestx:当前最佳路径的顺序 bestc:当前最佳路径的距离
    cc:当前路径的距离 n:城市的个数

    void Backtrack(int i){
    	if(i==n){ //对倒数第二层节点的处理
    		if(a[x[n-1]][x[n]] != NoEdge && a[x[n]][1] != NoEdge &&
    		(cc + a[x[n-1]][x[n]] + a[x[n]][1] < bestc || bestc == NoEdge)){
    			for(int j = 1;j <= n;j++) bestx[j] = x[j];
    			bestc = cc + a[x[n-1]][x[n]] + a[x[n]][1];	
    		}
    	}else{
    		for(int j = i;j <= n;j++){
    			if(a[x[i-1]][x[j]] != NoEdge &&
    			(cc + a[x[i-1]][x[j]] < bestc || bestc == NoEdge)){
    				Swap(x[i],x[j]);
    				cc += a[x[i-1]][x[i]];
    				Backtrack(i+1);
    				cc -= a[x[i-1]][x[i]];
    				Swap(x[i],x[j]);
    			}
    		}
    	}
    }

    作业调度

    使机器1没有空闲时间且机器2的空闲时间最小
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    M:各作业所需的处理时间 x:当前作业调度
    bestx:当前最优作业调度 f2:机器2完成处理时间
    f1:机器1完成处理时间 f:完成时间和
    bestf:当前最优值 n:作业数

    void Backtrack(int i){
    	if(i > n){
    		for(int j = 1;j <= n;j++) bestx[j] = x[j];
    		bestf = f;
    	}else{
    		for(int j = i;j <= n;j++){
    			f1 += M[x[j]][1];
    			f2[i] = ((f2[i-1]>f1)?f2[i-1]:f1)+M[x[j]][2]
    			f+=f2[i];
    			if(f < bestf){
    				Swap(x[i],x[j]);
    				Backtrack(i+1);
    				Swap(x[i],x[j]);
    			}
    			f1 -= M[x[j]][1];
    			f -= f2[i];
    		}
    	}
    }

    N皇后问题

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    bool Place(int k){
    	for(int j = 1; j < k;j++){
    		if((abs(k-j)==abs(x[j]-x[k])) || (x[j]==x[k])) return false;
    		return true;
    	}
    }
    void Backtrack(int t){
    	if(t > n) sum++;
    	else{
    		for(int i = 1;i <= n;i++){
    			x[t] = i;
    			if(Place(t)) Backtrack(t+1);
    		}
    	}
    }
文章作者: Davian
文章链接: https://daixinwang.github.io/2024/01/09/suan-fa-she-ji-yu-fen-xi-qi-mo-fu-xi/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Davian !
笔记 期末复习 算法
  目录